Optimising a Taskmaster Task with Python
For those that don’t know Taskmaster is a game show where 5 comedians compete in a variety of nonsensical tasks to win points from the Taskmaster. Most of the time the tasks are creative, (draw a horse while riding a horse) or time-based (burst all the bubbles on some bubble wrap in the shortest time). Still not sure what it is about? Watch some highlights on their Youtube channel here (hopefully, it works in your country).
Enjoy these types of posts? Then you should sign up for my newsletter.
It is my Thursday night ritual to settle down and watch this show and in a recent episode the final task set up an interesting problem that had some elements of game theory and randomness. It went as follows:
There are 100 balloons. 5 of the balloons are ‘bad’. You can throw between 1 and 10 darts to burst a balloon. If you burst one of the bad balloons you are eliminated. There are 5 contestants in total, if you are first eliminated you score 1 point, second eliminated 2 points, third eliminated 3 points, fourth eliminated then 4 points, and finally the winner scores 10 points.
I’ll walk you through how I simulated this task in Python, examined the different strategies and what the optimal strategy turned out to be. I’ll finally pose some open questions on where to take this next.
This is a task with some game theory, probability, and randomness, the type of thing that gets my grey matter active. Plus, one of the contestants (Victoria Coren Mitchel) is a professional poker player, so I wonder if she also had an idea on the best way to approach the task. If you only know VCM from Only Connect or being married to David Mitchell, read her book as it details her professional poker career.
How should you approach this balloon popping task? I hypothesised that early on in the game you want to throw as many darts as possible to try and force everyone else to hit one of the bad balloons. I picked up the pen and paper, tried to derive the probability distribution, gave up, and decided to play to my strengths. Which is applying some brute force with some computation.
Let’s start with setting up the right packages. All should be self-explanatory.
import random
import numpy as np
import pandas as pd
import seaborn as sns
sns.set_theme()
Now to get an idea of how to program this task we want to do the following.
- Draw 5 numbers from 1 to 100 without replacement. These represent the ‘bad balloon’ that will eliminate players.
- Draw all the numbers from 1 to 100 without replacement. This represents what order the balloons are popped.
- Find the index when the bad balloons are popped.
def simulate(balloons, bad):
bad_balloons = random.sample(range(balloons), bad)
throws = random.sample(range(balloons), balloons)
pops = [throws.index(x) for x in bad_balloons]
pops.sort()
return np.asarray(pops)
We can then run this 10,000 times and work out the average number if darts until each balloon is burst.
res = np.matrix([simulate(100, 5) for x in range(10000)])
res.sum(axis=0) / 10000
matrix([[15.8373, 32.7258, 49.4414, 66.3377, 83.1278]])
So, between 15 and 16 darts until the first balloon is popped, 33 until the second balloon (etc for the other balloons). So we can simulate the basic structure of the game, let’s now look at strategies.
Popping Strategies
We have a choice to throw \(N\) darts where \(1 \leq N \leq 10\). We can explore a null strategy, a constant strategy, and a ‘smart’ strategy.
- Null Strategy: Every time it is our turn, throw a random amount of darts.
- Fixed Strategy: Chose \(M\) darts, only ever throw this amount of darts.
- ‘Smart Strategy’: Adjust the number of darts you will throw based on whats happened in the game so far.
For each strategy, we will simulate the game multiple times and calculate the average points won to see how good it is.
Simulating the Task
We are now simulating the full game, so we need to take the simulate
function and slightly adjust it to account for the other players.
Whilst there are still balloons to be popped we go through each player and obtain the number of darts they want to through and then check to see if they hit a bad balloon. If they do hit a bad balloon, they are given a result and no longer participate. If all the balloons are popped the game finishes. For each game, we randomise the starting order of the players.
def run_game(throw_function):
bad_balloons = random.sample(range(100), 5)
bad_balloons.sort()
players = list(range(5))
burst = 0
total_throws = 0
result = [0 for x in players]
random.shuffle(players)
rewards = [1, 2, 3, 4, 10]
while burst <= len(bad_balloons):
for player in players:
throws = throw_function(player) if result[player] == 0 else 0
total_throws += throws
if total_throws >= bad_balloons[burst]:
total_throws = bad_balloons[burst]
result[player] = rewards[burst]
burst += 1
if burst >= len(bad_balloons):
break
if burst >= len(bad_balloons):
break
return(result)
For each of the listed strategies we want to create a throw_function
that we can pass into the run_game function that will play out that
game multiple times. We then calculate the average number of points
each player scores. We then refer to this as the expected points of
a strategy that someone would score if they played the task enough.
The Null Strategy
The null strategy is simple. We draw a random integer from between 1 and 10 to choose the number of darts to throw. Every player will follow this strategy and act randomly. We call it the null strategy as it doesn’t require any decisions and is the simplest approach to the game.
def null_strategy(player):
return random.sample(range(1, 10), 1)[0]
So to simulate this we pass the above function into our run_game
function.
null_results = np.matrix([np.asarray(run_game(null_strategy)) for x in range(100000)])
null_results.sum(axis=0) / 100000
matrix([[4.00084, 3.98669, 4.01453, 3.98103, 4.01691]])
This takes about 10 seconds and we can see that all 5 players on average earn about 4 points, the same as taking the average of all the points that could be rewarded.
The fact that everyone has close to the same amount of points, and these points are also close to the theoretical average reassures us that the above code is correct and is simulating the task properly. Always good to check these things!
The Constant Strategy
Now, let’s throw the same amount of darts per simulation. The other four players will throw a random amount, it is just us that will throw a fixed amount.
This time we are going to write a function that generates a function that helps keep the simulation code concise.
def constant_strategy_generator(strat):
def get_throws(player):
if player == 0:
return strat
return random.sample(range(1, 10), 1)[0]
return get_throws
We are player 0, so that’s when we throw strat darts. As an example,
we can generate a ‘throw 10’ function and pass that to the game
simulation and simulate the game 10 times.
throw10 = constant_strategy_generator(10)
res10 = np.matrix([np.asarray(run_game(throw10)) for x in range(100)])
res10.sum(axis=0) / 100
matrix([[2.67, 4.14, 4.8 , 4.32, 4.07]])
Our average points won of 2.67 is worse than the null strategy and worse than everyone else’s. Not a great sign for the ‘throw 10’ strategy.
Let’s run the simulation for all the values between 1 and 10 and pull out the results of player 0 (us!).
constant_results = [np.matrix([np.asarray(run_game(constant_strategy_generator(throws))) for x in range(100000)])[:, 0] for throws in range(1, 11)]
This takes about a minute and a half to run, so nothing too strenuous for my laptop.
We are now going to convert this to a pandas dataframe to allow easy plotting.
strat_results = np.concatenate(constant_results, axis=1)
strat_df = pd.DataFrame(strat_results, columns=[f'{throw}' for throw in range(1, 11)])
strat_df["Null"] = null_results[:, 0]
We’ve also added in the null result so can easily compare the strategies.
To plot the results we are going to use the seaborn package. This
allows us to summarise the results and calculate uncertainty in the
values automatically. In this case though, because of the large number
of simulations, you can’t see the error bars.
sns.catplot(data=strat_df, kind="point", join=False)
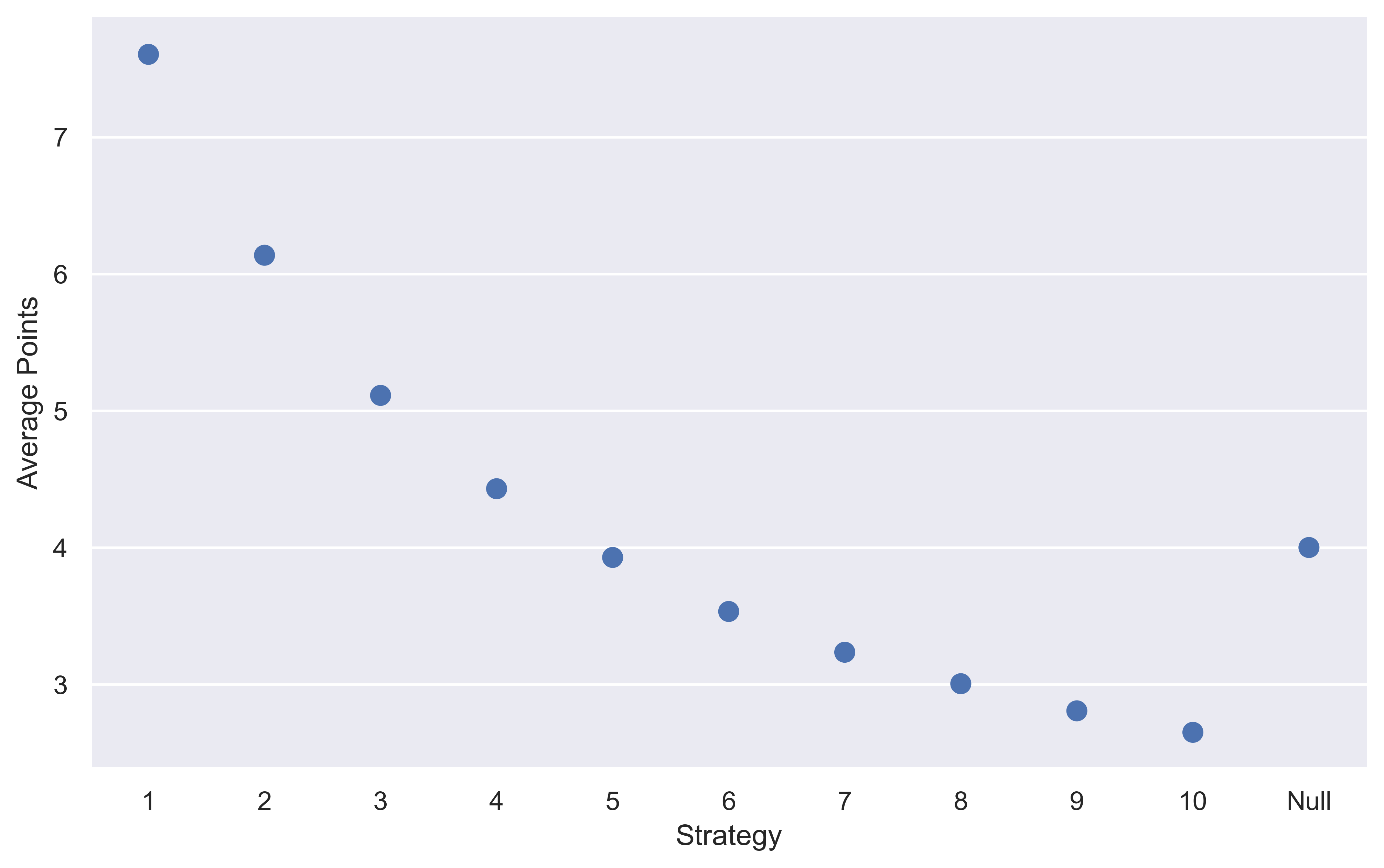
A couple of key things to point out here:
- The null result is comparable to always throwing 5 darts.
When randomly throwing darts, on average you will throw 5 darts, so again, this shows that our simulation is consistent.
- Throwing 1 dart is the best move.
With expected points of about 7.6, it’s easily the best way to maximise your point-scoring.
- Throwing any more than 5 darts is a negative expected value strategy.
So my original hypothesis was wrong, you don’t want to throw that many darts. Quite the opposite, minimise the number of darts you throw to score more points.
Now, can we vary the number of darts we throw in a smart way to arrive at a superior strategy?
An Intelligent Strategy
From the above, we know that you don’t want to throw that many darts, but, if we throw some more darts, reducing the number of balloons, there is a higher probability the other players will burst one of the bad balloons. When do we push our luck? When the probability of bursting a balloon is the lowest, which is the first round of the game (if you go first) or if you are next after a balloon bursts. So if we count the number of balloons since the last bad balloon burst we can pass that into our strategy and use it to decide how many to throw.
def intelligent_strat(darts_since_burst):
return 2 if darts_since_burst == 0 else 1
def throw_function_intelligent(player, darts_since_burst):
if player == 0:
return intelligent_strat(darts_since_burst)
return random.sample(range(1, 10), 1)[0]
Annoyingly, we now have to rewrite our simulation code to account for this extra variable we are passing in.
def run_game_intelligent(throw_function):
bad_balloons = random.sample(range(100), 5)
bad_balloons.sort()
players = list(range(5))
burst = 0
total_throws = 0
darts_since_burst = 0
result = [0 for x in players]
random.shuffle(players)
rewards = [1, 2, 3, 4, 10]
while burst <= len(bad_balloons):
for player in players:
throws = throw_function(player, darts_since_burst) if result[player] == 0 else 0
total_throws += throws
darts_since_burst += throws
if total_throws >= bad_balloons[burst]:
total_throws = bad_balloons[burst]
result[player] = rewards[burst]
burst += 1
darts_since_burst = 0
if burst >= len(bad_balloons):
break
if burst >= len(bad_balloons):
break
return(result)
Very similar to the previous simulation code, but now we also count the number of throws since the last bad balloon popped and pass that into our strategy function.
Again, we simulate this and add it to our results dataframe.
res_intelligent = np.matrix([np.asarray(run_game_intelligent(throw_function_intelligent)) for x in range(100000)])
res_intelligent.sum(axis=0) / 100000
strat_df["Smart"] = res_intelligent[:, 0]
strat_plot = sns.catplot(data=strat_df[['1', '2', 'Null', 'Smart']],
kind="point",
join=False, ci="sd")
This time instead of plotting the bootstrap errors we are plotting the standard deviation of the results which gives us an idea of the variance of the strategies.
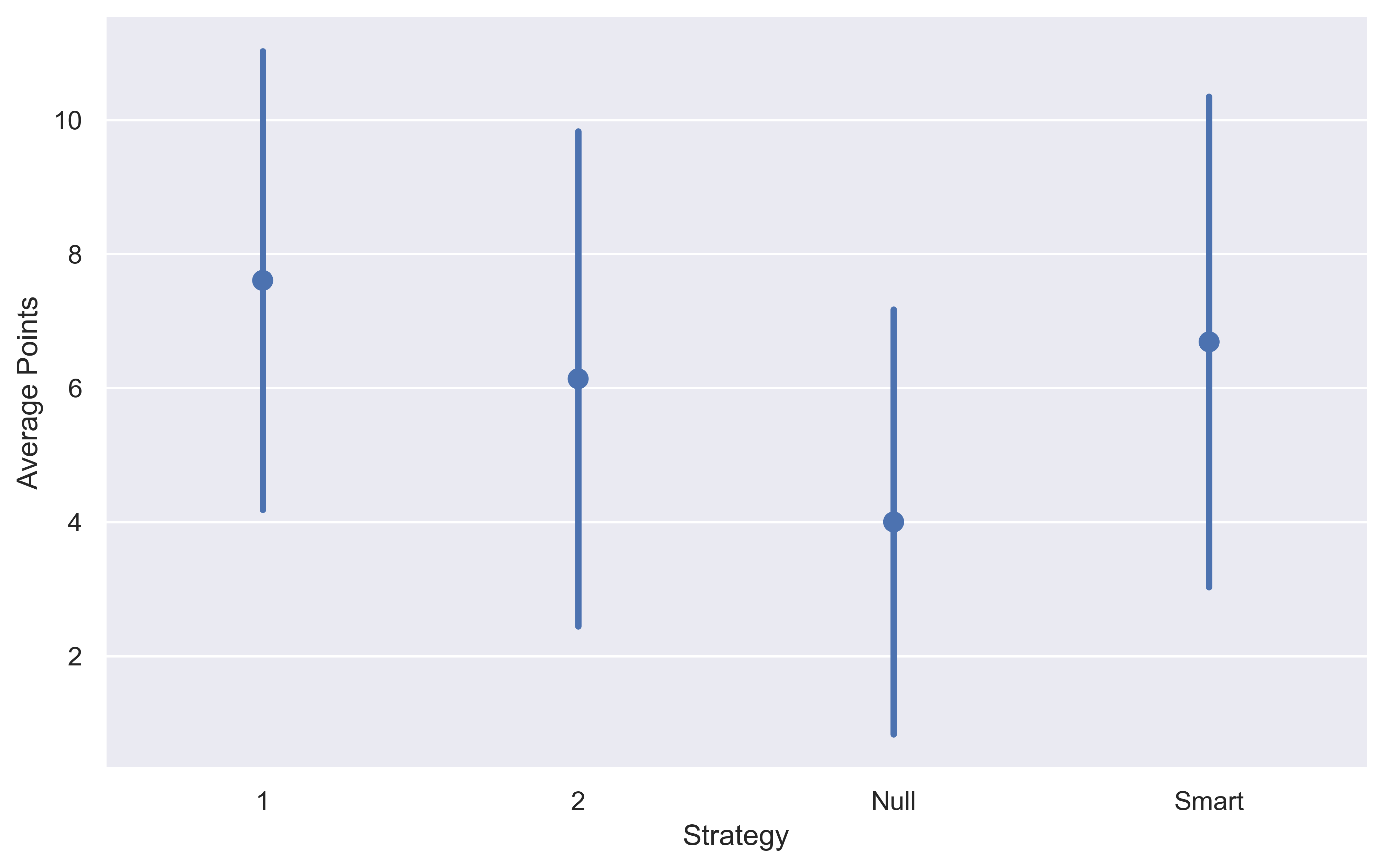
Disappointingly, still doesn’t improve on the constant 1 dart strategy, both in terms of average points and also variance. The 1 dart strat has a standard deviation of 3.42, whereas this smart strat has a standard deviation of 3.53.
Summary
For this Taskmaster task, your best bet is to throw one dart at a time. Bit of a boring result, but aligns with Occam’s razor, you don’t want to burst a balloon, so take part in the game as little as possible by throwing the least amount of darts.
Now, we could try and learn the optimal function by representing the strategy as a black box using a neural network, simulating through the task, and learning the optimal policy. But I don’t think there is much of a chance of improving on the simple 1 dart strategy because it is such a simple game.
Now, if I’ve made any glaring errors, written something inefficiently or you think you’ve come up with a better strategy, let me know in the comments below!