How to Calculate Realised Volatility

Volatility measures the scales of price changes and is an easy way to describe how busy markets are. High volatility means there are periods of large price changes and vice versa, low volatility means periods of small changes. In this post, I’ll show you how to calculate realised (realized) volatility and demonstrate how it can be used. If you just want a live view of crypto volatility, take a look at cryptoliquiditymetrics where I have added in a new card with the volatility over the last 24 hours.

Enjoy these types of posts? Then you should sign up for my newsletter.

To start with we will be looking at daily data. Using my CoinbasePro.jl package in a Julia we can get the last 300 days OHLC prices.

I’m running Julia 1.7 and all the packages were updated using Pkg.update() at the time of this post.

using CoinbasePro
using Dates
using Plots, StatsPlots
using DataFrames, DataFramesMeta
using RollingFunctions

From my CoinbasePro.jl package, we can pull in the daily candles of Bitcoin. 86400 is the frequency for daily data. Coinbase restrict you to just 300 data points so our period of time will be the previous 300 days.

dailydata = CoinbasePro.candles("BTC-USD", now()-Day(300), now(), 86400);
sort!(dailydata, :time)
dailydata = @transform(dailydata, :time = Date.(:time))
first(dailydata, 4)

4 rows × 7 columns

	close	high	low	open	unix_time	volume	time
	Float64	Float64	Float64	Float64	Int64	Float64	Date
1	50978.6	51459.0	48909.8	48909.8	1615075200	13965.2	2021-03-07
2	52415.2	52425.0	49328.6	50976.2	1615161600	18856.3	2021-03-08
3	54916.4	54936.0	51845.0	52413.2	1615248000	21177.1	2021-03-09
4	55890.7	57402.1	53025.0	54921.6	1615334400	28326.1	2021-03-10

Plotting this gives you the typical price path of daily closing prices. Now realised volatility is a measure of how varied this price was over time. Was it stable or were there wild swings?

plot(dailydata.time, dailydata.close, label = :none, 
     ylabel = "Price", title = "Bitcoin Price", titleloc = :left, linewidth = 2)

Bitcoin Daily Prices

To calculate this variation, we need to add in the log-returns.

dailydata = @transform(dailydata, :returns = [NaN; diff(log.(:close))]);
bar(dailydata.time[2:end], dailydata.returns[2:end], 
    label=:none, 
    ylabel = "Log Return", title = "Bitcoin Log Return", titleloc = :left)

Bitcoin Daily Log Returns

We can start by looking at this from a distribution perspective. If we assume the log-returns (\(r\)) are from a normal distribution, with zero mean, the standard deviation of this distribution is the equivalent to the volatility

\[r \sim N(0, \sigma ^2),\]

so \(\sigma\) is how we will refer to volatility. From this, you can see how high volatility leads to wide variations in prices. Each log-return sample has a wider range of values that it could be.

So by taking the running standard deviation of the log-returns we can estimate the volatility and how it changes over time. Using the RollingFunctions.jl package this is a one-liner.

dailydata = @transform(dailydata, :volatility = runstd(:returns, 30))
plot(dailydata.time, dailydata.volatility, title = "Bitcoin Volatility", titleloc = :left, label=:none, linewidth = 2)

Bitcoin Daily Volatility

There was high volatility over June this year as the price of Bitcoin crashed. It’s been fairly stable since then, hovering around 0.03 and 0.04. How does this compare though to the S&P 500 as a general indicator of the stop market? We know Bitcoin is more volatile than the stock market, but how much more?

I’ll load up the AlphaVantage.jl package to pull the daily prices of the SPY ETF and repeat the calculation; adding the log-returns and taking the rolling standard deviation.

using AlphaVantage, CSV

stockPrices = AlphaVantage.time_series_daily("SPY", datatype="csv", outputsize="full", parser = x -> CSV.File(IOBuffer(x.body))) |> DataFrame
sort!(stockPrices, :timestamp)
stockPrices = @subset(stockPrices, :timestamp .>= minimum(dailydata.time));

Again, add in the log-returns and calculate the rolling standard deviation to estimate the volatility.

stockPrices = @transform(stockPrices, :returns = [NaN; diff(log.(:close))])
stockPrices = @transform(stockPrices, :volatility = runstd(:returns, 30));

volPlot = plot(dailydata.time, dailydata.volatility, label="BTC", 
               ylabel = "Volatility", title = "Volatility", titleloc = :left, linewidth = 2)
volPlot = plot!(volPlot, stockPrices.timestamp, stockPrices.volatility, label = "SPY", linewidth = 2)

Bitcoin and SPY volatility

As expected, Bitcoin volatility is much higher. Let’s take the log of the volatility to look zoom in on the detail.

volPlot = plot(dailydata.time, log.(dailydata.volatility), 
               label="BTC", ylabel = "Log Volatility", title = "Log Volatility", 
               titleloc = :left, linewidth = 2)
volPlot = plot!(volPlot, stockPrices.timestamp, log.(stockPrices.volatility), label = "SPY", linewidth = 2)

Bitcoin and SPY Log Volatility

Interestingly the SPY has had a resurgence in volatility as we move towards the end of the year. One thing to point out though is the slight difference in look back periods for the two products. Bitcoin does not observe weekends or holidays, so 30 rows previously are always 30 days, but for SPY this is the case as there are weekends and trading holidays. In this illustrative example, it isn’t too much of an issue, but if you were to take it further and perhaps look at the correlation between the volatilities, this is something you would need to account for.

A Higher Frequency Volatility

So far it has all been on daily observations, your classic dataset to practise on. But I am always banging on about high-frequency finance, so let’s look at more frequent data and understand how the volatility looks at finer timescales.

This time we will pull the 5-minute candle bar data of both Bitcoin and SPY and repeat the calculation.

Calculate the log-returns of the close to close bars
Calculate the rolling standard deviation by looking back 20 rows.

minuteData_spy = AlphaVantage.time_series_intraday_extended("SPY", "5min", "year1month1", parser = x -> CSV.File(IOBuffer(x.body))) |> DataFrame
minuteData_spy = @transform(minuteData_spy, :time = DateTime.(:time, dateformat"yyyy-mm-dd HH:MM:SS"))
minuteData_btc = CoinbasePro.candles("BTC-USD", maximum(minuteData_spy.time)-Day(1), maximum(minuteData_spy.time),300);

combData = leftjoin(minuteData_spy[!, [:time, :close]], minuteData_btc[!, [:time, :close]], on=[:time], makeunique=true)
rename!(combData, ["time", "spy", "btc"])
combData = combData[2:end, :]
dropmissing!(combData)
sort!(combData, :time)
first(combData, 3)

3 rows × 3 columns

	time	spy	btc
	DateTime	Float64	Float64
1	2021-12-29T20:00:00	477.05	47163.9
2	2021-12-30T04:05:00	477.83	46676.3
3	2021-12-30T04:10:00	477.98	46768.8

For 5 minute data, we will use a look-back period of 20 rows, which gives us 100 minutes, so a little under 2 hours.

combData = @transform(combData, :spy_returns = [NaN; diff(log.(:spy))],
                                :btc_returns = [NaN; diff(log.(:btc))])
combData = @transform(combData, :spy_vol = runstd(:spy_returns, 20),
                                :btc_vol = runstd(:btc_returns, 20))
combData = combData[2:end, :];

Plotting it all again!

vol_tks = minimum(combData.time):Hour(6):maximum(combData.time)
vol_tkslbl = Dates.format.(vol_tks, "e HH:MM")

returnPlot = plot(combData.time[2:end], cumsum(combData.btc_returns[2:end]), 
                  label="BTC", title = "Cumulative Returns", xticks = (vol_tks, vol_tkslbl),
                  linewidth = 2, legend=:topleft)
returnPlot = plot!(returnPlot, combData.time[2:end], cumsum(combData.spy_returns[2:end]), label="SPY",
                   xticks = (vol_tks, vol_tkslbl),
                   linewidth = 2)


volPlot = plot(combData.time, combData.btc_vol * sqrt(24 * 20), 
    label="BTC", xticks = (vol_tks, vol_tkslbl), titleloc = :left, linewidth = 2)
volPlot = plot!(combData.time, combData.spy_vol * sqrt(24 * 20), label="SPY", title = "Volatility",
               xticks = (vol_tks, vol_tkslbl), titleloc = :left, linewidth = 2)

plot(returnPlot, volPlot)

5 minute returns and volatility

On the left-hand side, we have the cumulative return of the two assets on the 30th of December, and on the right the corresponding volatility. Bitcoin still has higher volatility whereas SPY has been relatively stable with just some jumps.

Simplifying the Calculation

Rolling the standard deviation isn’t the efficient way of calculating the volatility and can also be simplified down to a more efficient calculation.

The standard deviation is defined as:

\[\sigma ^2 = \mathbb{E} (r^2) + \mathbb{E} (r) ^2\]

if we assume there is no trend in the returns so that the average is zero:

\[\mathbb{E} (r) = 0\]

then we get just the first term

\[\sigma ^2 = \frac{1}{N} \sum _{i=1} ^N r^2\]

which is simply proportional to the sum of squares. Hence why you will hear that the realised variance is referred to as the sum of squares.

Once again, let’s pull the data and repeat the previous calculations but this time adding another column that is the rolling summation of the square of the returns.

minutedata = CoinbasePro.candles("BTC-USD", now()-Day(1) - Hour(1), now(), 5*60)
sort!(minutedata, :time)
minutedata = @transform(minutedata, :close_close_return = [NaN; diff(log.(:close))])
minutedata = minutedata[2:end, :]
first(minutedata, 4)

minutedata = @transform(minutedata,
                                    :new_vol_5 = running(sum, :close_close_return .^2, 20),
                                    :vol_5 = runstd(:close_close_return, 20))
minutedata = minutedata[2:end, :]
minutedata[1:5, [:time, :new_vol_5, :vol_5]]

5 rows × 3 columns

	time	new_vol_5	vol_5
	DateTime	Float64	Float64
1	2021-12-30T13:40:00	3.05319e-6	0.00171371
2	2021-12-30T13:45:00	5.11203e-6	0.00139403
3	2021-12-30T13:50:00	5.11472e-6	0.00118951
4	2021-12-30T13:55:00	6.40417e-6	0.00107273
5	2021-12-30T14:00:00	6.55196e-6	0.00104028

vol_tks = minimum(minutedata.time):Hour(8):maximum(minutedata.time)
vol_tkslbl = Dates.format.(vol_tks, "e HH:MM")

ss_vol = plot(minutedata.time, sqrt.(288 * minutedata.new_vol_5), titleloc = :left, 
              title = "Sum of Squares", label=:none, xticks = (vol_tks, vol_tkslbl), linewidth = 2)
std_vol = plot(minutedata.time, sqrt.(288 * minutedata.vol_5), titleloc = :left, 
               title = "Standard Deviation", label=:none, xticks = (vol_tks, vol_tkslbl), linewidth = 2)
plot(ss_vol, std_vol)

Standard deviation vs sum of squares for volatility

Both methods show represent the relative changes equally. There are some notable edge effects in the standard deviation method, but overall, our assumptions look fine. The y-scales are different though as there are some constant factor differences between the two methods.

Comparing Crypto Volatilities

Let’s see how the volatility changes across some different currencies. We define a function that calculates the close to close return and iterate through some different currencies.

function calc_vol(ccy)
    minutedata = CoinbasePro.candles(ccy, now()-Day(1) - Hour(1), now(), 5*60)
    sort!(minutedata, :time)
    minutedata = @transform(minutedata, :close_close_return = [NaN; diff(log.(:close))])
    minutedata = minutedata[2:end, :]
    minutedata = @transform(minutedata, :var = 288*running(sum, :close_close_return .^2, 20))
    minutedata
    minutedata[21:end, :]
end

Let’s choose the classics BTC and ETH, the meme that is SHIB and finally EURUSD (the crypto version).

p = plot(legend=:topleft, ylabel = "Realised Volatility")
for ccy in ["BTC-USD", "ETH-USD", "USDC-EUR", "SHIB-USD"]
    voldata = calc_vol(ccy)
    vol_tks = minimum(voldata.time):Hour(4):maximum(voldata.time)
    vol_tkslbl = Dates.format.(vol_tks, "e HH:MM")
    plot!(voldata.time, sqrt.(voldata.var), label = ccy, 
          xticks = (vol_tks, vol_tkslbl), linewidth = 2)
end
p

Volatility comparison between different currencies.

SHIB has higher overall volatility. ETH and BTC have very comparable volatilities moving together. EURUSD has the lowest overall (as we would expect), but interesting to see how it moved higher just as the cryptos did at about 9 am.

An Update to CryptoLiquidityMetrics

So I’ve taken everything we’ve learnt here and implemented it into cryptoliquiditymetrics.com. It is a new panel (bottom right) and calculated all through Javascript.

Screenshot of cryptoliquiditymetrics.com

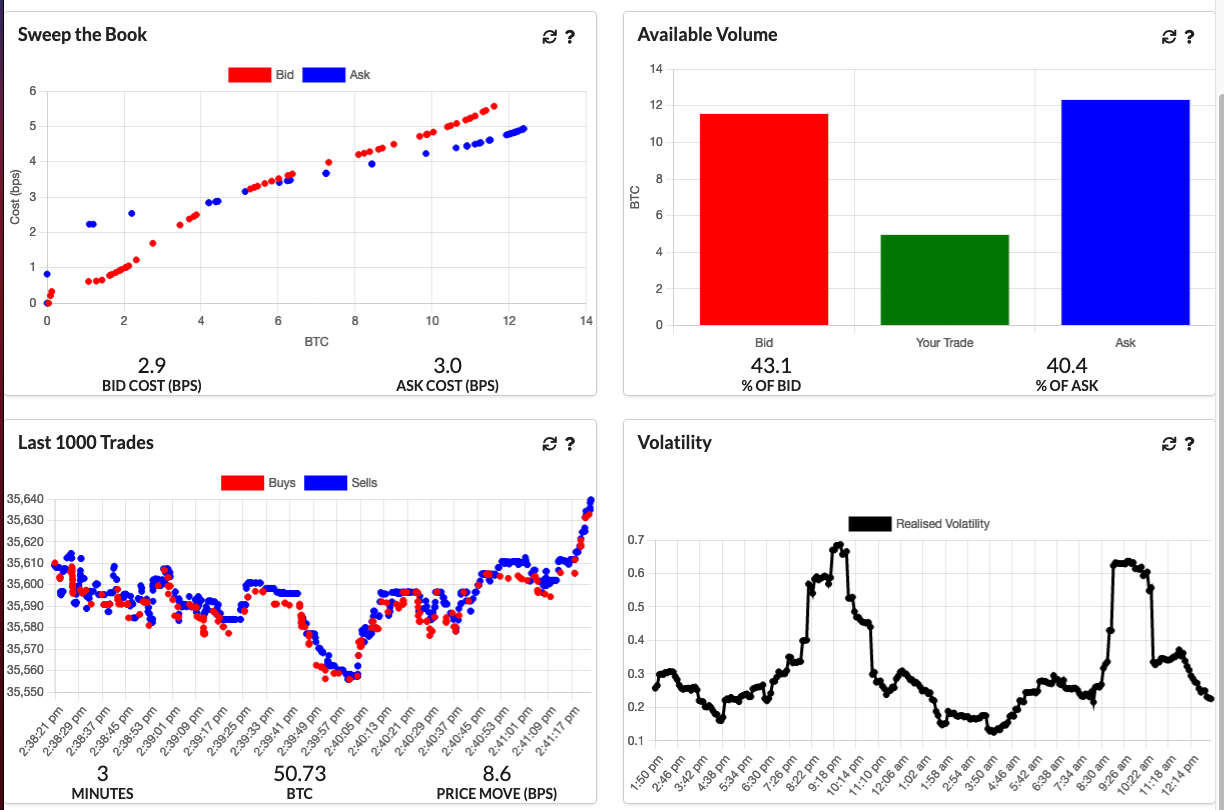
How does this help you?

Knowing the volatility helps you get an idea of how easy it is to trade or what strategy to use. When volatility is high and the price is moving about it might be better to be more aggressive and make sure your trade happens. Whereas if it is a stable market without too much volatility you could be more passive and just wait, trading slowly and picking good prices.

Just another addition to my Javascript side project!